

Lasaros
 Goumas
Goumas
Einleitung
Für jene, welche Elektronik nicht professionell einsetzten, sondern nur zur Lösung von sehr spezifischen Problemen benötigen, für die in der Regel „off the shelf electronic“ entweder nicht existiert oder sehr teuer ist, lohnt es sich, über den Einsatz von Mikrokontrollern Gedanken zu machen.
Bei der Entwicklung von Mikrokontrollern, wie zum Beispiel den PIC-Kontrollern der Firma Microchip, stand von vorn herein die Forderung nach schnellen und vor allem billigen Erzeugnissen im Vordergrund. Das war natürlich nur möglich, wenn man einen Prozessor mit einem einzigen Arbeitsregister und einem sehr eingeschränkten Befehlsvorrat definierte. Ein 8-Bit-PIC vom Typ 16F627A von Microchip verfügt über nur 35 unterschiedliche Befehle, kostet aber auch nur etwa2,- €.
Damit ist auch klar, dass man bei einem derart eingeschränkten Befehlsvorrat etc. nicht erwarten kann, dass man aufwendige mathematische Manipulationen mit Mikrokontrollern ohne weiteres durchführen kann. Erschwerend kommt hinzu, dass es sich für “Amateurentwickler“, welche auf eine möglichst große Transparenz für die Arbeitsweise des Kontrollers angewiesen sind, empfiehlt, ihre SW nicht mit Hochsprachen sondern in Assembler zu schreiben. Dies führt dann zwangsläufig dazu, dass eventuell in Hochsprachen vorhandene Algorithmen für aufwendige mathematische Manipulationen, in Assembler nicht zu finden sind.
In den nachfolgenden Abschnitten wird eine Sammlung von selbst entwickelten und getesteten mathematischen Algorithmen präsentiert. Für jede mathematische Operation wird eine Grundlagenbeschreibung, wo notwendig auch der Ablauf des Algorithmus in Pseudoassembler, und schließlich der Algorithmus selbst in Assembler aufgeführt.
1. Multiplikation
Multiplikationen erfolgen wie bei Dezimalzahlen durch Teiladditionen und Verschieben der Teilergebnisse. Im nachfolgenden Beispiel werden die Zahlen 0001 1011 x 0000 1001 (.27 x .9 = 243) im klassischen Verfahren miteinander multipliziert.

Das 8 Bit Ergebnis lautet dann: 1111 0011 (.243)
Wie aber oben bereits erläutert, ist aufgrund des stark eingeschränkten Befehlsvorrats der PICs die Durchführung einer klassischen, binären Multiplikation nicht möglich, und man muss deshalb für die Durchführung einer Multiplikation mit PICs Algorithmen verwenden, welche mit den vorhandenen Befehlssatz der PICs (Schiebe-/Additions- und Überlaufkontrollbefehle) auskommen.
Das hier vorgestellte Verfahren bedient sich folgender mathematisch korrekter Manipulationen.
Bei Beginn der Multiplikation muss das Ergebnisregister auf Null gesetzt werden.
Eine Verschiebung des Multiplikators um eins nach rechts (Halbierung des Multiplikators) und eine gleichzeitige Verschiebung des Multiplikanden um eins nach links (Verdopplung des Multiplikanden) beeinflusst nicht das Multiplikationsergebnis, solange die halbierten Werte des Multiplikators ganze Zahlen sind, d.h. kein Überlauf dabei entsteht.
Entsteht beim Verschieben des Multiplikators ein Überlauf (der halbierte Wert ist keine ganze Zahl), so muss der zuletzt nach links verschobene Wert des Multiplikanden dem Ergebnis zugezählt werden.
Die genannte Prozedur wird solange durchgeführt, bis der am Anfang auf 8 gesetzter Zykluszähler (die zu multiplizierende Werte sind 8 Bit breit) auf Null herunter gezählt ist.
Zum besseren Verständnis der Vorgehensweise wird ein PDF Dokument unter dem Titel „Multiplikationssubroutine in Pseudoassembler“ beigefügt.
PDF Dokument: "Multiplikationssubroutine in Pseudoassembler"
Bevor man sich allerdings an die Erstellung solcher Algorithmen heranwagt, sollte man sich zunächst einmal über das Umwandeln von "Nachkommazahlen" im Klaren sein.
Das Stellenwertsystem lässt sich rechts vom Komma logisch fortsetzen: Die erste Stelle nach dem Komma repräsentiert die Vielfachen von b(hoch-1) = 1/b zur Zahlenbasis b, die zweite Stelle die Vielfachen von b(hoch-2) = 1/b² usw.
Beispiel: Die Binärzahl 0,1011 entspricht der Summe der Brüche
1/2+0/4+1/8+1/16 = 0,5+0,125+0.0625 = 0.6875
Nachfolgend ein Beispiel für die Multiplikation von zwei Festkommazahlen in binärer 8-bit-Darstellung mit 4 Nachkommastellen und Schiebeoperation, wie sie in Rechnerarchitekturen üblicherweise verwendet wird.
Dezimal: 7,5x6,25=46,875
Mit nur 4 verfügbaren Nachkommastellen erreicht man folgendes Ergebnis: 0111,1000 x 0110,0100 binär entsprechend 7,5 x 6,25 = 46,875 dezimal

Das Ergebnis bei einer 8-Bit Festkommadarstellung mit 4 Nachkommastellen ohne Schiebeoperation wäre: 1110,0000 binär entsprechend 14,0 dezimal und damit unbrauchbar.
Nach einer Schiebeoperation von insgesamt 8 Kommastellen (ermittelt aus der Summe der Kommastellen von Multiplikand und Multiplikator) erhält man als Ergebnis:
010 1110,1110 binär entsprechend 46,875 dezimal was dem erwarteten Ergebnis entspricht.
1.1 Multiplikationsalgorithmen
Nachfolgend werden einige bereits getestete Multiplikationsalgorithmen im PDF vorgestellt.
1.1.1 Multiplikation von zwei Ganzzahlen
Der Algorithmus führt beispielhaft eine Multiplikation der zwei Ganzzahlen 27 x 9 = 243 [(0001 1011) x (000 1001) = (1111 0011)] durch. Da der Multiplikator größer 15 (dezimal) ist, enthält der Algorithmus 8 Durchläufe, und es werden damit für die Durchführung der Multiplikationssubroutine 117 "instruction cyrcles" benötigt. Betreibt man den PIC mit einem 4MHz Oszilator, so nimmt die Multiplikationssubroutine 117µsec für sich in Anspruch.
Vertauscht man die Funktion der zu multiplizierenden Zahlen derart, dass die Zahl 9 der Multiplikator wird, so werden jezt nur noch 4 Durchläüfe (9<15) benötigt, und die Rechenzeit der Multiplikationsroutine vermindert sich auf 61µsec.
1.1.2 Multiplikation von zwei Zahlen mit Nachkommastellen
Der Algorithmus führt beispielhaft eine Multiplikation der zwei Zahlen 24,1 x 3,203 = 77,1923 (dezimal) durch.
Zunächst einmal empfiehlt es sich, hierbei den Multiplikator durch geeignete Komma Verschiebungen zu eine Ganzzahl umzuwandeln. Im vorliegenden Fall verändern sich die zu multiplizierende Zahlen wie folgt: 241 x 0,3203 (dezimal) bzw. 1111 0001 x 0101 0010 (Binär). Weiterhin ist es aufgrund der Tatsache, dass der Multiplikand 8 mal nach links rotiert werden muss, erforderlich, für ihn zwei 8-bit Register bereit zu stellen. Ein low-Register zur Aufnahme des Anfangswertes des Multiplikanden und ein high-Register, um seine beim Rotieren nach links entstehenden Überläufe aufzunehmen. Schließlich werden zwei weitere 8-bit Ergebnisregister benötigt. Ein L_Byte Register für die Aufnahme der Nachkommastellen und ein links davon positioniertes H_Byte Register, um den Wert der Ganzzahl des Ergebnisses aufzunehmen.
Der Multiplikationsalgorithmus liefert als Ergebnis den Wert 0x4D,0x32 (Hex) entsprechend 77,195313 (dezimal), wobei er für die Durchführung der Multiplikationssubroutine 146 "instruction cyrcles" benötigt. Betreibt man den PIC mit einem 4MHz Oszilator, so nimmt die Multiplikationssubroutine 145µsec für sich in Anspruch.
2. Division
Die einfachste Methode eine Division durchzuführen, ist den Nenner so oft vom Zähler abzuziehen bis das Ergebnis kleiner Eins wird. Zählt man die Anzahl der durchgeführten Subtraktionen, so bildet deren Gesamtzahl das Ergebnis der Division ab. Dieses Verfahren ist recht einfach, so lange der Zähler recht klein ist. Wird der Zähler größer als der Nenner, so wird dieses Verfahren sehr zeitaufwendig und damit unbrauchbar.
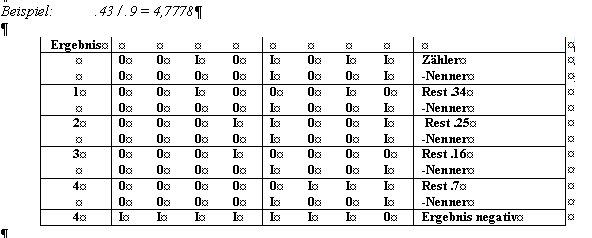
2.1. Ausführung einer allgemeinen Division mit einem 8-Bit PIC Mikrocontroller
Zur Ausführung einer allgemeinen Division mit einem 8-Bit PIC Mikrokontroller werden insgesamt 6 Register benötigt. Diese sind:
Zähler-Register
Nenner-Register
Rest-Register
Counter-Register (Zählregister zur Aufnahme der Anzahl der zu dividierenden Bits)
H_Byte (Register zur Aufnahme des Ganzzahlergebnisses der Division)
L_Byte (Register zur Aufnahme der Nachkommastellen des Divisionsergebnisses).
Bei Beginn der Division muss zunächst geklärt werden, ob das zu erwartende Divisionsergebnis größer oder kleiner Eins sein wird. Dies erfolgt durch eine Überprüfung, ob der Zähler größer oder kleiner als der Nenner ist.
Die Vorgehensweise für den Fall, dass der Zähler kleiner als der Nenner ist, ist wie folgt:
H_Byte und L_Byte werden gelöscht und das Counter Register auf 7 gesetzt.
Der Inhalt des Zähleregisters wird um 1 nach links rotiert und das Ergebnis wird wieder im Zähler gespeichert.
Anschließend wird der Nenner vom Zähler abgezogen.
Ist das Ergebnis der Subtraktion kleiner Eins, so muss Wert des Zählers vor der Subtraktion durch eine Addition des Nenners wieder hergestellt werden. Anschließend wird der Inhalt des L_Byte-Registers um 1 nach links rotiert, und der Stand des Counterregisters abgefragt. Ist der Counter auf Null so steht das Divisionsergebnis in L_Byte-Register. Trifft dies nicht zu, so gibt es einen neuen Durchlauf beginnend mit einer neuen Rotation des Inhaltes des Zähler Registers nach links.
Ist das Ergebnis der Subtraktion des Nenners vom Zähler größer Eins, so wird der LSB des L_Byte-Registers auf Eins gesetzt, sein Inhalt um 1 nach links rotiert, der Stand des Counterregisters abgefragt, und wenn er auf Null ist, kann das Divisionsergebnis in L-Byte-Register abgefragt werden. Trifft dies nicht zu, so gibt es einen neuen Durchlauf beginnend mit einer neuen Rotation des Inhaltes des Zählerregisters nach links.
Die Vorgehensweise für den Fall, dass der Zähler größer als der Nenner ist, ist zeitlich aufwendiger, weil diesmal zusätzlich zu den Nachkommastellen auch der Ganzzahlanteil in H_Byte-Register ermittelt werden muss.
Zu Beginn wird das Restregister gelöscht und der Counter auf 8 gesetzt.
Die Inhalte der Zähler- und Restregister werden um 1 nach links rotiert, wobei das MSB vom Zählerregister als LSB in das Restregister wandert.
Anschließend wird der Nenner vom Rest abgezogen und das Ergebnis wieder in R gespeichert.
Ist das Ergebnis der Subtraktion kleiner Eins, so muss der Wert des Restregisters vor der Subtraktion durch eine Addition des Nenners wieder hergestellt werden. Anschließend wird der Stand des um eins reduzierten Counterregisters abgefragt. Ist der Counter auf Null, so wird der Inhalt des Zählers als Ganzzahldivisionsergebnis in H_Byte-Register gespeichert. Trifft dies nicht zu, so gibt es einen neuen Durchlauf beginnend mit einer neuen Rotation der Inhalte von Zähler- und Restregistern nach links.
Ist das Ergebnis der Subtraktion des Nenners vom Rest größer Eins, so wird dem Zähler ein LSB zugefügt und der Inhalt des Counterregisters um Eins reduziert.. Ist der Counter auf Null, so wird der Inhalt des Zählers als Ganzzahldivisionsergebnis in H_Byte-Register gespeichert. Trifft dies nicht zu, so gibt es einen neuen Durchlauf beginnend mit einer neuen Rotation der Inhalte von Zähler- und Restregistern nach links.
Nach dem Setzen des Ganzzahldivisionsergebnisses im H_Byte-Register, erfolgt die Ermittlung des Inhaltes des L_Byte-Registers wie oben beschrieben, d.h. für den Fall, dass der Zähler kleiner als der Nenner ist.
Die beschriebene Vorgehensweise ist im nachfolgenden Diagramm erläutert.
PDF Dokument: "Divisionssubroutine in Pseudoassembler"
2.2. Divisionsalgorithmus für einem 8-Bit PIC Mikrocontroller in Assembler
Der Algorithmus führt beispielhaft die Division der Dezimalzahl 127 durch die Dezimalzahl 3 d.h. 127 / 3 = [(0111 111) / (0000 0011) = 42,333333. Als Ergebnis der Division erhält man im H_Byte-Register die dezimale Ganzzahl 42, und im L_Byte-Register den Nachkommadezimalanteil 84. Das Ergebnis lautet demnach: 42,329688. Für die Durchführung der Division werden 220 „instruction cycles“ benötigt. Betreibt man den PIC mit einem 4MHz Oszillator, so nimmt die Divisionssubroutine 215µsec für sich in Anspruch.
Vertauscht man Zähler mit Nenner (.3 / .127 = 0,023622), so erhält man im H_Byte-Register „0“ , und im L_Byte-Register den Nachkommadezimalanteil 6. Das Ergebnis lautet demnach: 0,023438. Für die Durchführung der Division werden 114 „instruction cycles“ benötigt. Betreibt man den PIC mit einem 4MHz Oszillator, so nimmt die Divisionssubroutine diesmal mit 111µsec erheblich weniger Rechenzeit für sich in Anspruch.
3. Trigonometrische Funktionen
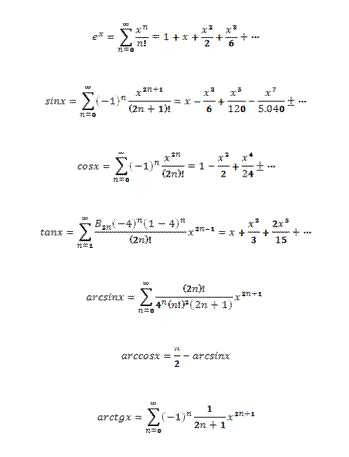
Nachfolgend wird die Bestimmung von trigonometrischen Funktionen mit Hilfe von Taylorreihen erläutert.
Das Konzept der Taylorreihen, entdeckt durch den schottischen Mathematiker James Gregory, wurde 1715 durch den englischen Mathematiker Brook Taylor formell eingeführt und deshalb nach ihm benannt.
Wenn, wie bei den trigonometrischen Funktionen, eine Taylorreihe sich um einen Nullpunkt konzentriert, so wird sie auch nach dem schottischen Mathematiker Colin Maclaurin, auch Maclaurinreihe, genannt.
Um den Rechenaufwand, bedingt durch die Beschränkung der Wortbreite der Mikrokontroller auf 8 Bit, erträglich gestalten zu können, muss man sich bei jeder Anwendung über die gewünschte Genauigkeit des Ergebnisses Gedanken machen, denn es ist nicht ungewöhnlich, dass Berechnungen von Taylorreihen - abhängig von der Anzahl der verwendeten Taylor Terms - durchaus Rechenzeiten von über einer Sekunde für sich in Anspruch nehmen können.
In dem nachfolgend erläuterten Beispiel - die Berechnung des Sinus eines Winkels - wird deutlich, dass eine Beschränkung der Taylorreihe auf zwei Terms durchaus brauchbare Ergebnisse liefern kann.
3.1. Sinusalgorithmus für einen 8-bit Mikrocontroller in Assembler
Der im PDF Dokument „SINUS“ beschriebene Algorithmus berechnet beispielhaft den Sinus des Winkels von 329,3° entsprechend -0,510543.
3.1.1. Eingabe des winkels
Die Nachkommazahl, hier 0,3, wird als Dezimalzahl (.3) im Nachkommaregister (wkomma) eingetragen. Da die Ganzzahl 329 mit einer 8 Bit Wortbreite nicht darstellbar ist, wird in ein High Bit Register (H_multkator) eine dezimale .1, und in ein Low Bit Register (L_multkator) die dezimale .73 eingetragen.
3.1.2 Transformation des Winkels in einem Winkel im ersten Quadranten
Da die Taylorreihen sich um einen Nullpunkt konzentrieren, ist es notwendig, den Winkel des zu berechnenden Sinus unter Berücksichtigung seines Vorzeichens zu einem äquivalenten Winkel im ersten Quadranten des Einheitskreises zu transformieren. Dies geschieht mit Hilfe der Subroutine „Quadrant“
Das Ergebnis des zu berechnenden Sinus, hier 30,7°, steht dann im Register „wgrad“ und sein Vorzeichen im Register „sign“, wobei die „0“ für ein negatives Vorzeichen steht.
3.1.3 Umwandlung des Winkelausdrucks inklusive Nachkomma zu einer Ganzzahl
Da der Winkel für die nachfolgend anstehenden Multiplikationsoperationen als Multiplikator verwendet wird, empfiehlt es sich, ihn inklusive seiner Nachkommastelle als Ganzzahl darzustellen.
Dies geschieht mit Hilfe der Subroutine „Winkel“. Hierbei wird die Ganzzahl für Grad mit 10 multipliziert und dazu wird die Nachkommastelle addiert. Das Ergebnis - hier 30x10+7 = 307 - wird mit einer .1 im „H_multkator“ Register und einer .51 im „L_multkator“ Register abgelegt.
3.1.4 Umwandlung des Winkels in Bogenmaß
Da die Taylorreihenterms sich auf das Bogenmaß des Winkels beziehen, muss die zu einer Ganzzahl umgewandelte Angabe des Winkels mit π multipliziert und durch 1.800 dividiert werden. Um sich auf Multiplikationsalgorithmen beschränken zu können, wird an Stelle der Division eine Multiplikation mit 1/1.800 eingeführt. Damit reduziert sich die Prozedur auf eine Multiplikation des Winkels mit dem Faktor 0,001745.
Diese Multiplikation geschieht mit Hilfe der Subroutine „bogenmass“. Da der genannte Multiplikationsfaktor von 0,001745 mit einem einzigen Multiplikanden Nachkommaregister wie „L_multkand“ nicht dargestellt werden kann - der Grenzwert dieses Registers würde bei 1/512 = 0,001953 liegen und wäre damit größer als 0,001745 - muss hier ein weiteres 8-Bit breites Nachkommaregister mit der Bezeichnung „LL_multkand“ eingeführt werden, welches beim Beginn des Hauptprogramms mit der Dezimalzahl .114 geladen wird. Damit erhält man im vorliegenden Fall einen Multiplikationsfaktor von 0,00174 und damit einen unwesentlich kleineren Wert als den geforderten von 0,001745.
Die Einführung des zusätzlichen rechten Nachkommaregisters des Multiplikanden müsste konsequenterweise auch zu einem weiteren rechten Nachkommaregister für das Ergebnis der Multiplikation führen. Da aber dieses Register das Gesamtergebnis hier unwesentlich beeinflusst, wird darauf verzichtet, und die Multiplikation wird mit nur einem 8-Bit Nachkommaregister für das Ergebnis durchgeführt.
Das Ergebnis der Multiplikation wird im konkreten Fall in dem „H_Byte“ Register in Form einer .0 und im „L_Byte“ Register in Form einer dezimalen .135 abgelegt. Das berechnete Bogenmaß lautet demnach 0,527344 und ist etwa um 1% kleiner als das erwartete Bogenmaß von 0,535816.
3.1.5 Ermittlung des Taylorterms x³/6
Dies geschieht mit Hilfe der Subroutine „taylor“ in drei aufeinander folgenden Multiplikationsschritten {[(x * x) * x] * (1/6)} wobei der Term x den „H_Byte“ und „L_Byte“ Registern entnommen wird. Das Ergebnis wird in den „H_taylor“ und „L_taylor“ Registern nieder gelegt.
3.1.6 Berechnung der Sinusfunktion
Dies erfolgt im Hauptprogramm und zwar durch Subtraktion der Werte der Taylorregister von denen der Byteregistern und wird in den Registern „H_sinus“ und „L_sinus“ abgelegt. Im konkreten Fall erhält man eine .0 im „H_sinus“ und eine dezimale .130 im „L_sinus“ Register und das Ergebnis lautet demnach: Sinus(30,7°) = 0,507813 und weicht unwesentlich vom theoretischen Wert von 0,510543 nämlich um etwa 0,5%. Der verwendete Algorithmus kann allerdings bei Berechnungen mit Winkeln in der Nähe von 90° durchaus Abweichungen von etwa 2% verursachen.
Für die Durchführung des Algorithmus werden 1.005 "instruction cycles" benötigt. Betreibt man den PIC mit einem 4MHz Oszillator, so nimmt die Gesamtroutine 981µsec für sich in Anspruch.
4. Zeitrechnung
4.1 Schaltjahr Berechnung
Wie im Teil II dieser Homepage (Mathematische und Astronomische Fundstücke) unter der Überschrift „Irritationen mit dem Schaltjahr“ beschrieben, wird bei der Berechnung, ob ein Jahr ein Schaltjahr ist oder nicht wie folgt vorgegangen:
Ist die Jahreszahl eines Jahres nicht durch „4“ teilbar, so handelt es sich zweifelsfrei nicht um ein Schaltjahr.
Ist die Jahreszahl eines Jahres zwar durch „4“ jedoch nicht durch „100“ teilbar, so handelt es sich zweifelsfrei um ein Schaltjahr.
Ist die Jahreszahl eines Jahres sowohl durch „4“ als auch durch „100“ jedoch nicht durch „400“ teilbar, so handelt es sich zweifelsfrei nicht um ein Schaltjahr.
Unter dem Begriff „Teilbar“ wird hier ein Divisionsergebnis verstanden, bei dem das Ergebnis durch eine Ganzzahl repräsentiert wird.
Die verwendete Routine ist im PDF Dokument „LEAPYEAR“ niedergelegt. Um den Rechenaufwand bei der Division zu reduzieren, wird der Divisionsalgorithmus nur für den Fall, der Zähler ist größer als der Nenner, verwendet, was dann dazu führt, dass die kleinste Jahreszahl,welche hier verarbeitet werden darf, größer 400 sein muss. Da wir aber bei solchen Rechnungen mit sehr großen Zahlen konfrontiert werden, wird die Rechnung mit 2x8 Bit Worten durchgeführt. Die demnach zugelassenen Jahreszahlen liegen im Bereich von 401 bis 65.535.
Für die Durchführung des Algorithmus werden im günstigsten Fall 840 "instruction cycles" benötigt. Betreibt man den PIC mit einem 4,096MHz Oszillator, so nimmt die Gesamtroutine 820µsec für sich in Anspruch. Im worst case jedoch benötigt der Microcontroller 2.750 „instruction cycles“, wobei man bei Verwendung eines 4,096MHZ Oszillators mit einer Gesamtdauer von 2,7msec rechnen muss.
neuer Text