

Lasaros
 Goumas
Goumas
Das Internet hält für seine Benutzer unzählige aktuelle Informationen zu alle denkbaren Themen bereit, und sollte deshalb zur Erweiterung oder Auffrischung der eigenen Kenntnissen extensiv genutzt werden. Dies gilt natürlich auch ganz besonderes für die Bereiche Mathematik und Astronomie.
Die Sonderstellung der Mathematik in der Naturwischenschaft
Archimedes
Pythagoras
Mathematik und Astronomie in der Antike - Rätsel und Lösungen
Der Absolute Beweis

Wer die Arbeiten der Mathematiker seit Pythagoras verstehen will, muss zu allererst den entscheidenden Unterschied zwischen der naturwissenschaftlichen und mathematischen Beweisführung begreifen. Denn die mathematische Beweisführung ist viel anspruchsvoller als die Beweisführung wie Physiker, Chemiker oder anderer Naturwissenschaftler sie verstehen und anwenden.
Um ein bestimmtes Phänomen erklären zu können, wird in den Naturwissenschaften zunächst eine Hypothese aufgestellt und eine Vielzahl von Beobachtungen, welche in engem Zusammenhang mit dem Phänomen stehen, durchgeführt. Die aufgestellte Hypothese sollte sich allerdings nicht nur auf die Beschreibung eines einzigen bekannten Phänomens beschränken, sonder auch Ergebnisse anderer Phänomene vorhersagen können. Stimmen die Beobachtungen mit der aufgestellten Hypothese überein, so wird dies zunächst einmal als ein erster Beleg für die Gültigkeit der Hypothese angesehen. Um die Vorhersagekraft der Hypothese auch für andere Phänomene überprüfen zu können, ist es allerdings erforderlich, Experimente durchzuführen. Verlaufen die Experimente ebenfalls positiv, so kann dies als ein weiterer Beleg für die Gültigkeit der aufgestellten Hypothese dienen. Eine große Menge von zutreffenden Beobachtungen und eine erdrückend hohe Anzahl von Experimenten mit positivem Ausgang wirken irgendwann einmal so beeindruckend, dass die aufgestellte Hypothese als naturwissenschaftliche Theorie anerkannt wird.
Der Werdegang der naturwissenschaftlichen Theorie, nämlich, dass sie auf eine endlicher Anzahl von Beobachtungen und Experimenten beruht, welche möglicherweise auch fehlbar sein könnten, deutet daraufhin, dass sie immer mit gewissen Zweifeln behaftet ist, und deshalb nur als höchstwahrscheinlich richtig gelten darf. In letzte Konsequenz sind daher alle Ergebnisse der Naturwissenschaft mit einem Makel, nämlich den der Ungewissheit behaftet. Dieser Schwäche des naturwissenschaftlichen Beweises verdanken wir allerdings die wissenschaftlichen Revolutionen, bei denen eine bis gestern geltende Theorie heute durch eine andere besser begründete oder sogar in Widerspruch zu ihr stehende Theorie ersetzt wird.
Die Vorgehensweise beim mathematischen Beweis ist jedoch eine völlig andere. Sie beginnt mit der Beschreibung von einer Reihe von Aussagen - Axiomen genannt - welche entweder als offensichtlich wahr angesehen werden oder deren Inhalt höchstwahrscheinlich wahr sein könnte. Durch die Entfaltung eines logischen Gedankenganges, also die Entwicklung von konsekutiven logischen Schritten, gelangt man zu einer Schlussfolgerung, welche dann Theorem oder Satz genannt wird. Der so geführte mathematische Beweis ist unbestreitbar und gilt für immer.
Das unvollständige Schachbrett

Dass Mathematik nicht auf fehlerbehaftete Experimente angewiesen ist, sondern auf unfehlbarer Logik beruht, lässt sich an der Lösung des Problems des unvollständigen Schachbretts eindrucksvoll demonstrieren.
Gegeben sei ein Schachbrett, dem zwei diagonal gegenüberliegende, weiße Felder fehlen, so dass es aus nur 62 Quadraten besteht. Vorhanden sind weiterhin 31 Steine, mit denen man jeweils zwei Quadrate exakt abdecken kann.
Frage: Ist es möglich, die 31 Steine so zu legen, dass sie alle 62 Quadrate des Schachbretts abdecken?
Beim naturwissenschaftlichen Ansatz würde man das Problem durch eine Reihe von experimentellen Ansätzen versuchen zu lösen. Man würde dabei vermutlich ziemlich schnell feststellen, dass keine Anordnung von Steinen gefunden werden kann, welche die genannte Fragestellung beantwortet. Aufgrund der großen Anzahl der Versuche wäre man geneigt, zu dem Schluss zu kommen, dass man hinreichend nachgewiesen hat, dass das Brett niemals vollständig abgedeckt werden kann. Man könnte jedoch niemals sicher sein, dass es nicht doch eine Anordnung von Steinen geben kann, welche man nicht ausprobiert hat und die das Brett vollständig abdeckt. Die Aussage, die Aufgabe ist nicht lösbar, ist also eine Theorie, welche auf einer beschränkten Anzahl von durchgeführten Experimenten basiert, und birgt demnach in sich die Gefahr, dass sie sich eines Tages als falsch erweist.
Der mathematischer Ansatz basiert jedoch auf der Entwicklung von logischen Argumenten, welche zu eine Schlussfolgerung führen, die zwingend richtig ist, und auch in der Zukunft niemals in Frage gestellt werden kann. Die Beweisführung würde dann wie folgt aussehen:
da per Definition dem Schachbrett zwei weiße Felder abgetrennt wurden, besteht es nun aus 32 schwarzen und 30 weißen Quadraten
jeder Stein bedeckt zwei benachbarte Quadrate, welche konstruktionsbedingt immer verschiedenfarbig sind
mit den ersten 30 Steinen werden 30 schwarze und 30 weiße, also insgesamt 60 Quadrate des Bretts abgedeckt
da die verbliebenen 2 Quadrate beide schwarz sind, aber der letzte Stein zwei verschiedenfarbige Quadrate abdecken müsste, die nicht vorhanden sind, ist die gestellte Aufgabe nicht lösbar
Die Zahl π im Kampf zwischen Ordnung und Chaos

Mathematische Regelmäßigkeiten, welche einem natürlichen Phänomen zugrunde liegen, wurden bereits durch Pythagoras entdeckt. Er hat auch gezeigt, dass es eine grundlegende Beziehung zwischen der Mathematik und naturwissenschaftlichen Phänomenen gibt, und dass diese Beziehung durch Zahlen ausgedrückt werden kann. Eine dieser Geheimnis umwitterten Zahlen ist die Zahl π, welche ursprünglich aus der Geometrie des Kreises abgeleitet wurde und seitdem immer wieder bei unterschiedlichen physikalischen Zusammenhängen auftaucht.
Diese Zahl scheint z.B. auch die Länge mäandernde Flüsse zu beeinflussen. Bildet man das Verhältnis zwischen der Gesamtlänge von Flüssen zu der Luftlinienentfernung zwischen ihrer Quelle und ihrer Mündung, so stellt man fest, dass dieses Verhältnis zwar von Fluss zu Fluss variiert, aber der Mittelwert dieses Verhältnisses, gebildet über eine ausreichende Anzahl von Flüssen, 3,14 beträgt, und damit erstaunlich nahe an die Zahl π herankommt.
Mit der Frage, warum Flüsse mäandern, hat sich auch Einstein beschäftigt. Er kam zu dem Schluss, dass Flüsse immer stärkere Windungen ausbilden müssen, weil die geringste Biegung in Stromrichtung die Geschwindigkeit der Strömung am Rand der Biegung erhöht, womit die Erosion am äußeren Rand begünstigt und damit der Radius der Biegung immer größer wird. Mit wachsendem Radius der Biegung, wächst aber auch erneut die Strömungsgeschwindigkeit an ihrem äußeren Rand, was zu einer Zunahme der Erosion und damit zu einer erneuten Vergrößerung des Radius der Biegung führt.
Es muss jedoch einen natürlichen Prozess geben, welcher dafür sorgt, dass irgendwann mal diesem aufschwingenden Chaos Einhalt geboten wird. Dies geschieht spätestens dann, wenn die Krümmung kreisförmig wird, und die Gefahr besteht, dass der Fluss kehrt macht und zu seinem Ursprung zurückzufließen versucht. Der Fluss muss nun geradeaus fließen, und die Biegung wird ein toter Arm. Die Zahl π ist demnach möglicherweise nichts anderes als eine Folge des Kampfes zwischen Ordnung und Chaos.
Der Codex von Archimedes

Am Donnerstag den 29 Oktober 1998 fand in den Räumen von „Christie´s in New York die Versteigerung des Gebetbuches des griechischen Mönches Ιωάννη Μύρωνα welcher im 13. Jahrhundert in Jerusalem lebte, statt. Den Zuschlag für dieses Buch, dessen Mindestpreis mit 800.000 $ beziffert war, erhielt für 2.200.000 $ ein Bekannter Buchhändler aus Mailand, welcher seinen Auftraggeber nie genannt hat. Er hat nur bestätigt, dass es sich um einen US-Bürger handelte, der jedoch nicht Bill Gates war. Die Vertreter der griechischen Regierung, welche auch großes Interesse an dem Buch hatten, stiegen beim Preis von 1.900.000 $ aus.
Das große Interesse für das Buch resultierte aus der Tatsache, dass trotz des katastrophalen Zustandes des Buches, Spuren eines älteren Textes sichtbar waren, hinter denen man eines der wichtigsten Werke von Archimedes vermutete, welches als definitiv verloren galt. Und in der Tat aufwendige Rekonstruktionsarbeiten brachten den Codex C von Archimedes in Form eines Palimpsest ans Licht.
Da Schreibmaterial wie Pergament sehr kostbar war, wurden beschriebene Manuskriptseiten häufig wieder verwendet. Das Wort Palimpsest setzt sich aus den Worten πάλιν (erneut) und ψέω (reiben/ kratzen) zusammen. Dabei wurde das Geschriebene abgekratzt bzw. abgewaschen. Auch wurden bereits chemische Tintenkiller wie Zitronensäure verwendet, um die Tinte zu entfernen. Die meisten Palimpseste bestehen aus Pergament oder Papyrus. Spuren des Originaltextes sind oft erhalten und können heutzutage häufig mittels Fluoreszenzfotografie sichtbar gemacht werden, so dass das Lesen des alten Textes wieder möglich wird. Viele antike und mittelalterliche Texte sind nur als eine solche „Schrift unter der Schrift“ überliefert und daher lückenhaft.
Die Schriften von fast allen altgriechischen Gelehrten existieren heute nur in Form von Abschriften, welche im 9. und 10. Jahrhundert in Konstantinopel erstellt wurden. Die Werke von Archimedes bilden da keine Ausnahme. Es handelt sich um Abschriften genannt Codex A, B und C. Hier sollte allerdings festgehalten werden, dass manche Abhandlungen durchaus sowohl in Codex A, B, oder C vorkommen können.
Die Abhandlung „Περί επιπέδον ισορροποιών“ (Ebenen Gleichgewicht) ist in jedem Codex enthalten
Codex A und Codex B enthalten die Abhandlung über den „Τετραγωνισμό της παραβολής“ (Quadratur der Parabel)
Codex A und Codex B enthalten die Abhandlungen über „Περί σφαίρας και κυλίνδρου, κύκλου μετρησις, και περί ελίκων“ (Kugel, Zylinder, Vermessung des Kreises und Schrauben)
Codex B und Codex C enthalten die Abhandlung „Περί οχουμένων“ (Über schwimmende Körper)
Codex A ist die einzige Quelle „ Περί κωνοειδέων και σφαιροειδέων και του Ψαμμίτη“ (Über Konoide, Sphäroide und die Sandrechnung)
Codex C ist schließlich die einzige Quelle für die „Μέθοδο και το Στομάχιον“ (Methode und das Ostomachion, was in der arabischen Überlieferung zu Stomachion verstümmelt wurde)
Unglücklicherweise gibt es für den Codex A und B keine Originale, und wir verfügen heute nur über Kopien und Übersetzungen, welche mindestens 400 Jahre später entstanden sind. Codex C ist demnach das einzige handschriftliche Dokument, welches die Abhandlungen über „Περί επιπέδον ισορροποιών, Περί οχουμένων, την Μέθοδο και το Στομάχιον“ in Griechisch beinhaltet.
Pythagoras der Philosoph und Mathematiker der religiöse Lehren verkündete

Pythagoras von Samos war ein antiker griechischer Philosoph und Gründer einer einflussreichen religiös-philosophischen Bewegung. Als Vierzigjähriger verließ er seine griechische Heimat und wanderte nach Kroton (heute Crotone im unteritalienischen Kalabrien) aus. Dort gründete er eine Schule, deren Mitglieder eine enge Gemeinschaft bildeten und sich auf eine disziplinierte, bescheidene Lebensweise festlegten (pythagoreische Art des Lebens) und sich zur Treue gegeneinander verpflichteten.
Trotz intensiver Bemühungen der Forschung gehört er noch heute zu den rätselhaftesten Persönlichkeiten der Antike. Manche Historiker zählen ihn zu den Pionieren der beginnenden griechischen Philosophie, Mathematik und Naturwissenschaft, andere meinen, er sei vorwiegend oder ausschließlich ein Verkünder religiöser Lehren gewesen. Möglicherweise konnte er diese Bereiche verbinden. Die nach ihm benannten Pythagoreer blieben auch nach seinem Tod kulturgeschichtlich bedeutsam.
Als es zu Unruhen in Kroton kam und die Unmut der Bürger sich gegen die Pythagoräer richtete, übersiedelte Pythagoras nach Metapontion (heute Metaponto in der Basilicata), wo er den Rest seines Lebens verbrachte.
Da keine Schriften des Pythagoras überliefert sind, stößt eine Rekonstruktion seiner Lehre auf große Schwierigkeiten. Die uns bekannte antike Überlieferung besteht größtenteils aus späten Quellen. Die antiken Hinweise und Berichte sind voller Widersprüche und stark von Legenden durchsetzt. Das Ziel vieler Autoren war die Verherrlichung des Pythagoras, einige wollten ihn verunglimpfen. Daher gehen trotz intensiver Klärungsbemühungen noch heute die Meinungen der Forscher auch über Grundlegendes weit auseinander.
War nun Pythagoras ein religiöser Führer mit geringem oder keinem Interesse an Wissenschaft, oder in erster Linie Philosoph, Mathematiker und Naturwissenschaftler? Manche Philosophiehistoriker suchen eine mittlere Position zwischen den beiden Richtungen, und nicht alle, welche die eine These ablehnen, sind Verfechter der anderen.
Der Gegensatz zwischen den verschiedenen Forschungsrichtungen zeigt sich auch in einzelnen umstrittenen Punkten:
Der Beweis für den Satz von Pythagoras
Die meisten veröffentlichten mathematischen Beweise sind oft so kompliziert, dass Laien den hierzu benötigten logischen Schritten kaum folgen können. Eine Ausnahme bildet allerdings der von Pythagoras für die Gültigkeit seines pythagorischen Theorems formulierte Beweis, dessen Ziel es war, zu zeigen, dass der genannte Satz für alle rechtwinkligen Dreiecke gilt.
Die Details des vorgelegten Beweises, dieses Meilensteins in der Entwicklung der Mathematik, sind im PDF Dokument „Der Beweis für den Satz von Pythagoras“ niedergelegt.
PDF Dokument: "Der Beweis fuer den Satz von Pythagoras"
Inkommensurabilität oder die Pythagoreische Grundlagenkrise

Den Pythagoräern wird oft eine „Zahlenmystik“ mit dem Grundsatz „Alles ist Zahl“ angelastet. Diese Haltung resultiert aus der Behauptung, dass, wo wir auch hin schauen, überall Zahlen sehen: Zwei Bäume, fünf Menschen, drei Steine, acht Schafe etc. Die Zahlen begründen demnach unsere Weltordnung, wobei der Zahl „Eins“ eine besondere Bedeutung zukommt, weil aus ihr alle anderen Zahlen sich zusammensetzen (2=1+1 oder 4=1+1+1+1). Da nun die Zahl 1 der Ursprung aller anderen Zahlen ist, wird sie deshalb einer Gottheit gleichgesetzt.
Fragte man Pythagoras nach den Dezimalzahlen, wie z.B. die 1,5 so erhielt man als Antwort: Auch die 1,5 ist eine reelle Zahl, welche als Ergebnis des Bruchs von zwei ganzen Zahlen entstanden ist, wie z.B. 1,5=3/2, wobei die ganzen Zahlen des Bruchs-, die Zahlen 3 und 2-, wiederum aus der „Eins“ entstanden sind. Demnach kann jede Dezimalzahl durch die Zahl "eins" erzeugt werden.
Diese Behauptung geriet allerdings ins Wanken, als ein Schüler von Pythagoras, der Metapontier Hípassos mit dem Theorem seines Lehrers, - dem uns bekannten Pythagorischen Theorem, wonach in einem rechtwinkligen Dreieck das Quadrat der Hypotenuse exakt gleich der Summe der Quadrate der zwei senkrecht aufeinander stehenden Seiten ist -, experimentierte.
Hípassos stellte nun die Frage nach dem Quadrat der Hypotenuse, für den Fall wenn die Größe von beiden senkrecht aufeinander stehenden Seiten gleich „Eins“ ist. In diesem Fall müsste das Quadrat der Hypotenuse gleich 1+1 sein. Es muss demnach eine Zahl geben, welche bei der Multiplikation mit sich selbst 2 ergibt. Heute wissen wir, das dies die Wurzel von 2 ist, also eine irrationale Zahl, und als solche durch ganzzahlige Zahlenverhältnisse nicht ausdrückbar (Inkommensurabilität).
Híppasos hat damit die Grundlage der pythagoreischen Mathematik in Frage gestellt, die besagte, alle Phänomene seien als Erscheinungsformen ganzzahliger Zahlverhältnisse erklärbar. Es wird auch behauptet, dass durch die Entdeckung der mathematischen Irrationalität, Híppasos die Pythagoräer in eine schwere Krise gestürzt habe. Eine späte Überlieferung behauptet, Híppasos habe diese Entdeckungen veröffentlicht und damit aus der Sicht der Pythagoräer Geheimnisverrat begangen. Daraufhin sei er aus der Gemeinschaft ausgeschlossen worden und bei einem Schiffunglück unter mysteriösen Umständen umgekommen, was als göttliche Strafe zu deuten sei.
Die Staufer und die Einführung Arabischen Zahlen in Europa
Europa hat der staufischen Herrschaft in Sizilien eine Menge interessante Neuerungen zu verdanken. Leonardo Pisano, genannt Fibonacci, führte unter dem Einfluss arabischer Mathematiker in Friedrichs II. Vielvölkerstatt Sizilien die Arabische Zahlen und das Dezimalsystem in Europa ein. Friedrich II. gründete unter anderem in Neapel eine Universität, deren Mediziner und Mathematiker einen ausgezeichneten Ruf genossen.
Der Antikythera Mechanismus

Der Mechanismus von Antikythera, oft auch Computer von Antikythera genannt, ist ein antikes Artefakt aus Zahnrädern, das einem Uhrwerk ähnelt. Es wurde in einem Schiffswrack vor der griechischen Insel Antikythera, gefunden und zunächst auf das Jahr 82 v. Chr. datiert. Im Jahr 2006 durchgeführte Untersuchungen der Schriftzeichen lassen jedoch Vermutungen auf eine Nutzung des Apparates 15 bis 20 Jahre vor diesem Datum zu. Das Schiff wurde auf Grund der Funde erst auf 80 v. Chr., heute auf bis 150 v. Chr. datiert.
Das Wrack des griechischen Handelsschiffs vor Antikythera wurde Ostern 1900 in einer Tiefe von etwa 40 Metern gefunden. Zahlreiche Statuen und andere Kunstschätze wurden geborgen und in das Archäologische Nationalmuseum nach Athen gebracht. Dort entdeckte der Archäologe Valerios Stais am 17. Mai 1902 in einem Klumpen aus korrodiertem Material ein Zahnrad.
Der Mechanismus, hergestellt aus Bronze und wahrscheinlich ursprünglich von einem Holzgehäuse umgeben, ist die älteste erhaltene Zahnrad-Apparatur. Der Fund hat unter Wissenschafts- und Technik-Historikern große Irritationen ausgelöst. Am meisten Akzeptanz hat die Theorie gefunden, den Mechanismus als eine Art Analogrechner zu verstehen, dessen Zweck darin bestand, die Bewegungen der Himmelskörper zu berechnen. Neuere funktionierende Rekonstruktionen der Apparatur bestätigen diese These. Das Gerät ist besonders erstaunlich, weil es ein Differentialgetriebe enthält, das nach der herkömmlichen Meinung erst im 13. Jahrhundert erfunden wurde.
Eine Zusammenfassung der neusten Forschungsergebnisse können der PDF Datei "Das Uhrwerk“ entnommen werden.
Irritationen mit dem Schaltjahr
Als Schaltjahr (annus bissextus) wird ein Jahr im Kalender bezeichnet, das im Unterschied zum Normaljahr in einem Schaltmonat einen zusätzlichen Schalttag enthält.
Im Unterschied zu einem Mondkalender richtet sich ein Sonnenkalender nach dem Lauf der Sonne. Das davon bestimmte tropische Jahr hat eine Länge von 365,24219 Tagen. Diesem Wert kommen die nachfolgend beschriebenen Sonnenkalender mit Hilfe von Einschaltungen mehr oder weniger nahe.
Julianischer Kalender
Unter Gaius Iulius Caesar wurde im Jahre 45 v. Chr der bis dahin geltende römische Kalender durch das Einfügen eines Schalttages reformiert. Der Schalttag wurde in jedem vierten Jahr dem Monat Februar hinzugefügt, und zwar am 24. Februar, d.h. 6 Tage vor den Kalenden des März (ante diem sextum calendas martias).
Das julianische Kalenderjahr hatte danach eine durchschnittliche Länge von 365,25 Tagen. Verglichen mit dem astronomischen (tropischen) Jahr betrug der Fehler dieses Kalenders einen Tag in etwa 128 Jahren.
GregorianischerKalender
1582 fand entsprechend dem Julianischen Kalender das astronomische Ereignis der ersten Tag-und-Nacht-Gleiche (Primaräquinoktium) im Jahr schon am 11. März statt, also 10 Tage früher als an dem Datum wie es für den Frühlingsanfang - nämlich den 21. März - während des ersten Konzils von Nicäa im Jahr 325 festgelegt worden war.
Papst Gregor XIII. ließ deshalb zum Ausgleich dieser aufgelaufenen Differenz von 10 Tagen im Jahr 1582 auf den 4. Oktober den 15. Oktober folgen, wobei die Abfolge der Wochentage nicht verändert wurde; auf einen Donnerstag folgte ein Freitag.
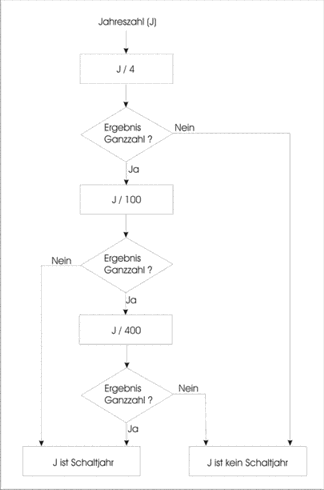
Die Schaltjahrregel im Gregorianischen Kalender besteht nun aus drei Regeln, wobei die ersten zwei vom julianischen Kalender übernommen wurden:
1. Die durch 4 ganzzahlig teilbaren Jahre sind Schaltjahre. Danach wären z.B. die nachfolgenden Jahre 1600, 1700, 1800, 1900, 2000, 2008, 2012 und 2100 eigentlich alle Schaltjahre.
2. Die durch 100 ganzzahlig teilbaren Jahre sind jedoch in der Regel keine Schaltjahre. Es blieben von den im vorliegenden Beispiel genannten Jahren nur 2008 und 2012 als Schaltjahre übrig.
3. Doch sind die ganzzahlig durch 400 teilbaren Jahre nun ebenfalls Schaltjahre. Damit sind 1600 und 2000 jeweils auch Schaltjahre.
Das gregorianische Kalenderjahr hat eine durchschnittliche Länge von 365,2425 Tagen. Der Fehler hat sich auf einen Tag in mehr als 3000 Jahren verringert, so dass voraussichtlich erst im Jahre 4800 ein Schalttag zusätzlich entfallen muss, um das Kalenderdatum 21. März in der Nähe des Zeitpunkts des Primar-Äquinoktiums zu positionieren.
Auch nach der Einführung des gregorianischen Kalenders war es noch eine Zeit lang üblich, in einem Schaltjahr den 24. Februar zu verdoppeln. Inzwischen geschieht dies jedoch durch die Einführung des 29. Februar als Schalttag.
Die Regeln zur Errechnung eines Schaltjahres sind im nebenstehenden Flussdiagramm niedergelegt.